
Solving algebra equations often involves solving for a value or an unknown variable, such as "x". You can find this value or unknown variable when you follow the rules for solving. Those rules include using the order of operations.
The order of operations provides procedures for solving equations. It tells you what to do first, second, third, and so on. We'll discuss the order of operations later, but first, we need to discuss balanced equations!
Keeping Equations Balanced

Equations are like balance scales. Just as balance scales must have the same weight on either scale to remain balanced, equations must have the same value on either side to remain balanced. Adding something to only one side causes the scale or balance to tip.
Think of the equal sign as the balancer in an equation. What is listed on the left side must equal or balance to what is listed on the right side.
Balanced Equation Example:
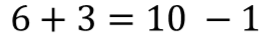
This equation is balanced because each side equals 9 when the operations are performed.
Unbalanced Equation Example:
 This equation is unbalanced because each side totals a different amount.
This equation is unbalanced because each side totals a different amount.
But what about an equation with a variable?
The same rule applies to equations containing variables. Using the examples shown above, let's replace one of the values on the left side with a variable.
Examples:
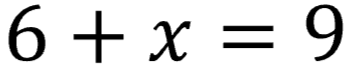 In this equation, 6 must be added to 3 for the equation to equal 9.
In this equation, 6 must be added to 3 for the equation to equal 9.
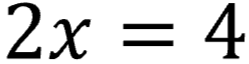 In this equation, 2 must be multiplied by 2 for the equation to equal 4.
In this equation, 2 must be multiplied by 2 for the equation to equal 4.
These equations remain equal or balanced even though there is now a variable.
The "x" value in each equation must equal the value that will make the equation true and keep the equation balanced.
Note: In each of these equations, the right side of the equation was simplified.
Undoing Operations

Sometimes algebra equations require a bit more work to find the value of the "x" variable. This is where undoing operations comes in.
 Undoing operations means:
Undoing operations means:
Isolating the variable. Isolating means getting the variable by itself without any number values.
Balancing the equation. The variable needs to be on one side of the equal sign while all known values should be on the other side.
Performing inverse operations on both sides. Inverse operations are doing the opposite operation to cancel something out.
 In our previous examples, the variable (or unknown value) is added in one equation and multiplied in the other. If we performed the inverse or opposite operations in each equation, we would subtract (inverse of addition) in the first equation and divide (inverse of multiplication) in the second.
In our previous examples, the variable (or unknown value) is added in one equation and multiplied in the other. If we performed the inverse or opposite operations in each equation, we would subtract (inverse of addition) in the first equation and divide (inverse of multiplication) in the second.
 Some common operations and their inverses:
Some common operations and their inverses:
Addition and subtraction


Multiplication and division


The square of a number and the square root of a number

Note: When taking square roots, we take both a positive AND a negative number since a negative times a negative is positive.
This list can be used both ways for algebra equations — meaning if you're subtracting, you'll add, etc.
Let's apply this to some examples!
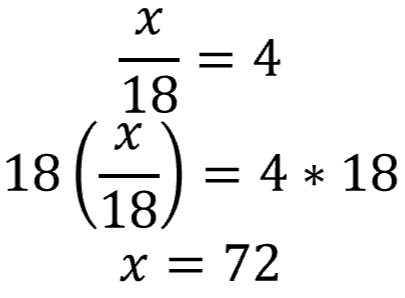
Here we multiplied both sides by 18 (undoing the division by 18).
Notice that the 18s cancel each other out... and the other side equals the value of "x"
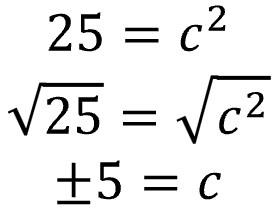
Here we took the square root of each side (undoing the c-squared term).
Notice that the square and square root cancel each other out for "c"... and the other side equals the value of "c"

The phrase "cancels each other out" means that the values either zero out (return a value of 0) or that the values result in 1 (return a value of 1). For example, -5 + 5 returns a value of 0, and 4/4 returns a value of 1.
Equations with More Than One Operation

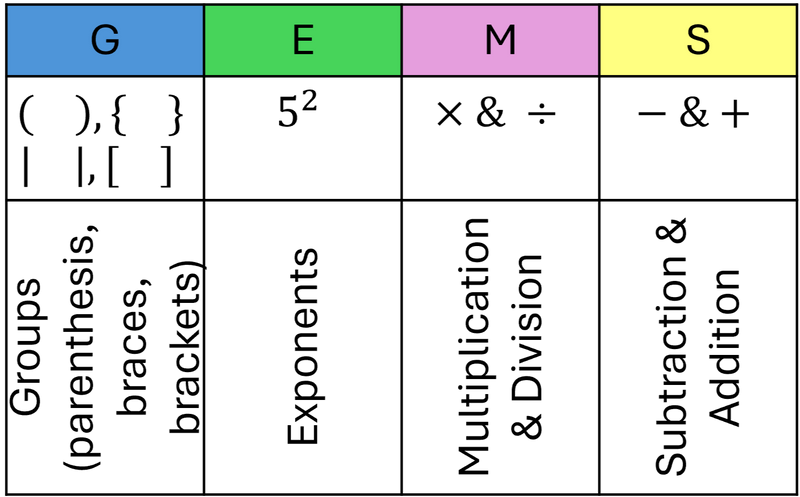
These acronyms work by performing operations in order: parenthesis (or groups), exponents, multiplication & division (from left to right) then addition & subtraction (from left to right) when NO variables are in the equation.
For Example:

 When solving for a variable we will reverse our order of operations. Instead of beginning with parenthesis or groups (unless we need to distribute), we begin with subtraction or addition then multiplication or division, and so on. Let's have a look!
When solving for a variable we will reverse our order of operations. Instead of beginning with parenthesis or groups (unless we need to distribute), we begin with subtraction or addition then multiplication or division, and so on. Let's have a look!
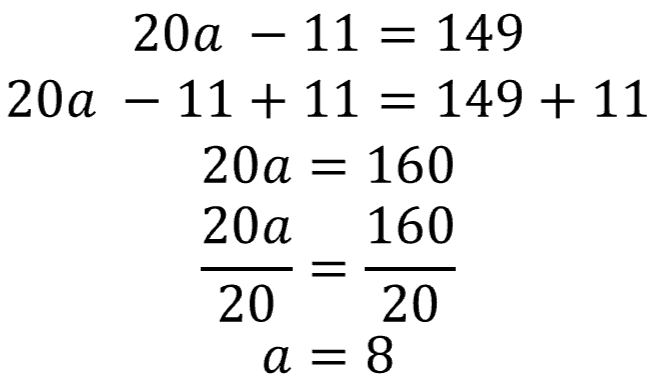
Begin by adding 11 to both sides —undoing the operation of subtraction (the "S" in PEMDAS or GEMS). This zeros out 11 on one side and adds it to the other.
Then divide both sides by 20 (the "D" in PEMDAS or "M" in GEMS) — undoing the multiplication to the variable "a", bringing its value to 1.
Quiz
You are given the equation x^2 = 100 (x squared equals 100). How would you undo the operation?
Try Some Problems for Yourself!
You'll find the answers in the "Did you know" section below!
Problem 1
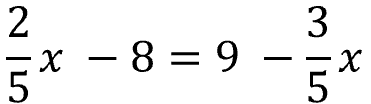
Hint: Treat the fractions with the variable as a set. Add/Subtract them from both sides as a set (Example: add 3/5x to both sides).
Problem 2
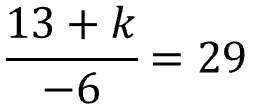
Hint: Begin by undoing the division with multiplication.
Problem 3
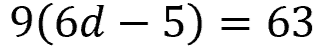
Hint: Begin by distributing (multiplying) the 9 to everything inside the parenthesis.
Problem 4
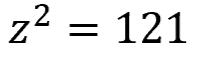
Hint: Remember, the inverse of squaring is taking the square root. When taking square roots, remember to take a positive number AND a negative number since a negative times a negative gives you a positive.
Take Action
 Practice solving equations with and without a variable or unknown value. Remember to use the order of operations to guide you in solving the equation!
Practice solving equations with and without a variable or unknown value. Remember to use the order of operations to guide you in solving the equation!
Visit these other Bytes if you need additional help with algebra equations:
Your feedback matters to us.
This Byte helped me better understand the topic.





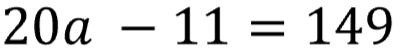 Enter the order of operations!
Enter the order of operations!