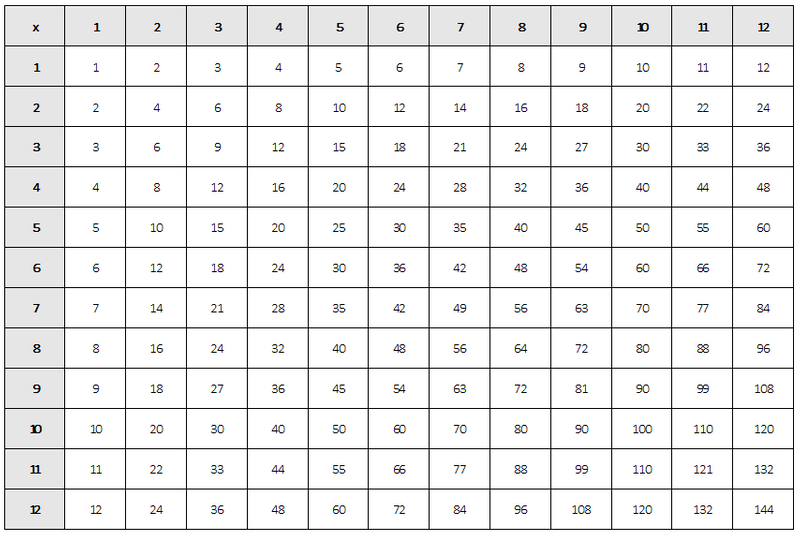
Multiplication is a shortcut to adding. Think of it as a way to add numbers without doing it over and over again.
You can say 2 + 2 + 2, or you can say 2 x 3 (that is, 3 sets of 2) and get the same answer: 6.

Working with larger numbers gets more difficult.
For example, it'll be more work to add 9 + 9 + 9 than to multiply 9 x 3!

If you haven't memorized your multiplication tables, then multiplying 9 x 3 may be hard for you! This is where a multiplication chart can help.
Multiplication charts can also help with fractions and division too!

Which tables do you not have to learn? Dinner tables!
Finding Patterns
Patterns are like the building blocks of math skills!
They show relationships between things and can help you understand numbers. Our very number system is a pattern based on multiplying by 10! For example, 100 is 10 times bigger than 10.
You can find a bunch of number patterns in a multiplication chart! Patterns are repeated lineups of numbers.
Look at these patterns:
Even Number Pattern

Do you know what seems odd? Numbers that aren’t divisible by 2!
Odd Number Pattern

Did you notice that the odd numbers chart fills in the spaces in the even numbers chart?
Square Number Pattern
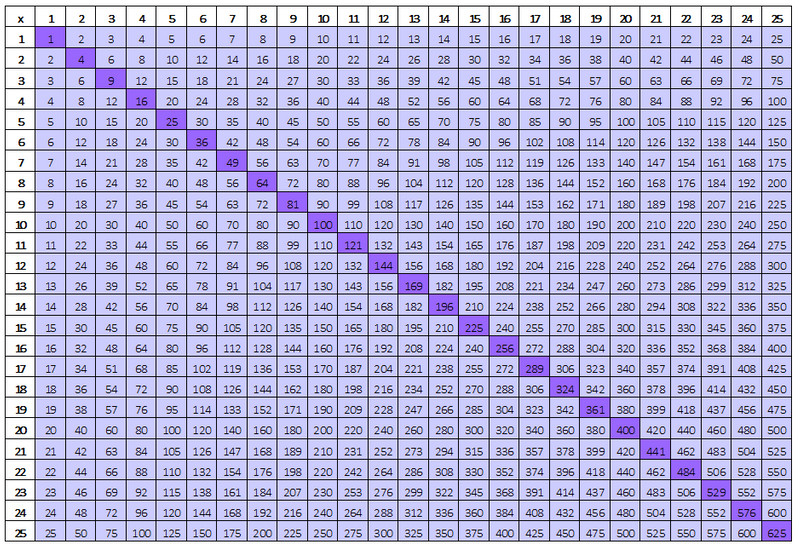

Notice the diagonal line down the center? These are square numbers:
2² (or "2 squared") = 2 x 2 = 4
3² (or "3 squared") = 3 x 3 = 9, and so on
Compare the numbers on either side of the diagonal line that runs across the chart above.

Do you see the numbers are mirrored? The same numbers are on both sides of the diagonal!
What other patterns can you find?
Use these ideas to get you started:
Times Tables
Starting with 1 x 1, color in the answer (product) and all the blocks on the same row/column
Then color in the row/column answer to 2 x 2 with a different color
Then 3 x 3 and so on (see the sneak peek below)
What pattern does this make?
 Answer: It makes "L-shapes" or an arrow, depending on how you look at it!
Answer: It makes "L-shapes" or an arrow, depending on how you look at it!
Boxed Numbers
Pick a number on the chart
Color the numbers around it to form a box (see the sneak peek below)
Add and subtract the corner numbers or the numbers above/below
Multiply and divide the corner numbers or the numbers above/below
What do you notice when you add/subtract or multiply/divide the numbers?
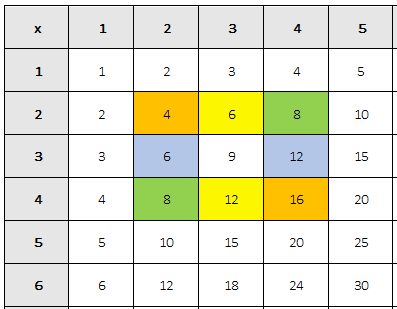 Answer: Some of your answers are the numbers around the center number! Most of the numbers can be divided by 4.
Answer: Some of your answers are the numbers around the center number! Most of the numbers can be divided by 4.
Answer #3: adding/subtracting
Corner numbers:
16 + 4 = 20
8 + 8 = 16
16 - 4 = 12
8 - 8 = 0
Above/below numbers:
12 + 6 = 18
12 - 6 = 6
Answer #4: multiplying/dividing
Corner numbers:
16 x 4 = 64
8 x 8 = 64
16/4 = 4
8/8 = 1
(Above/below numbers:
12 x 6 = 72
12/6 = 6
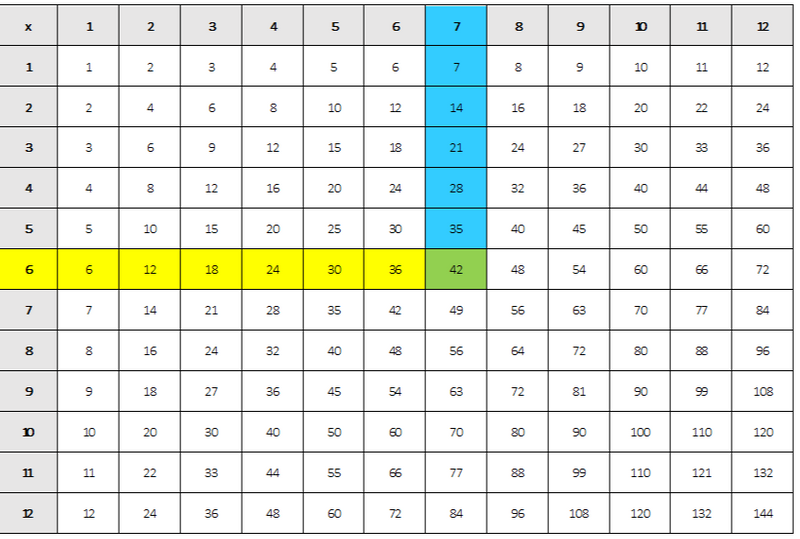
Mutliplying Numbers
What tool is best suited for math? Multi-pliers!
 Multiplication charts can help you easily find the product of two numbers.
Multiplication charts can help you easily find the product of two numbers.
Here's how...
Work in rows and columns. Try multiplying 6 x 7:
Find 6 in the first column
Move along the row until you come to the 7 column
The number where the 6 row and 7 column meet is the product of 6 x 7, which is 42
 Challenge
Challenge
See if you get the same answer when you choose 7 from the first column then follow the row to the 6 column!
Dividing Numbers
Multiplication charts can also help you with dividing numbers.

Start by finding the number you're dividing, then follow the row/column that made that number. For example, if you want to know what two numbers or factors multiply to get 40:
Find 40 on the chart
Move up the column and across the row to get the numbers 8 and 5 — these are the factors of 40
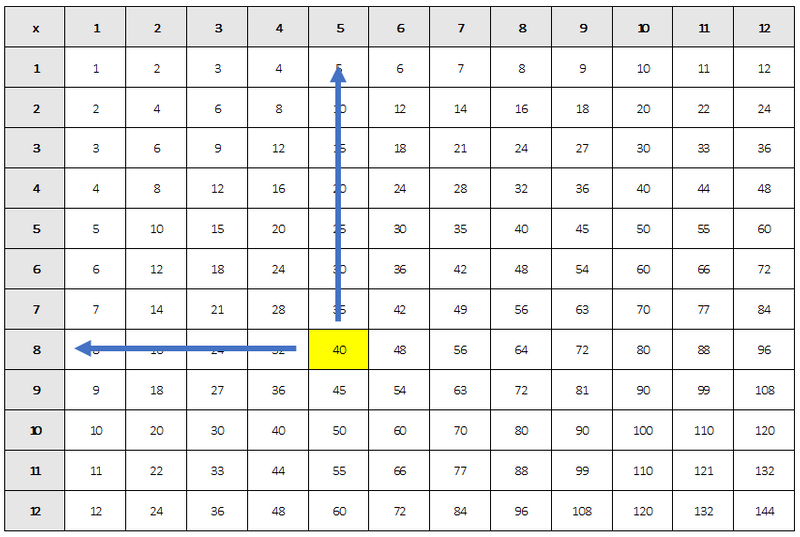
 Challenge:
Challenge:
Do you see any other blocks with 40 on the chart? What factors do you get when you move along those rows/columns?
Quiz
What other factors multiply to get 40? Select all that apply:
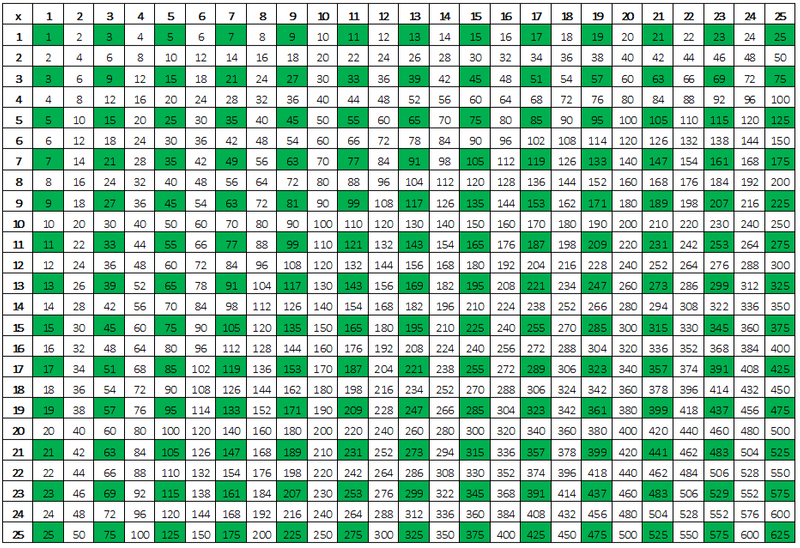
Reducing Fractions
Need to reduce a fraction? A multiplication chart can help with that!

Fractions are just division problems in disguise. And, we learned how to divide using a mutliplication chart in the last section.
Take a look at a division symbol...now replace the dots with numbers and presto, you have a fraction!

You can find this same pattern in a multiplication chart! This means you can use a multiplication chart to find and reduce fractions!
To reduce a fraction using the multiplication chart...
Find the fraction in the chart — just look down the columns
Move along the rows to the left to find the reduced fraction
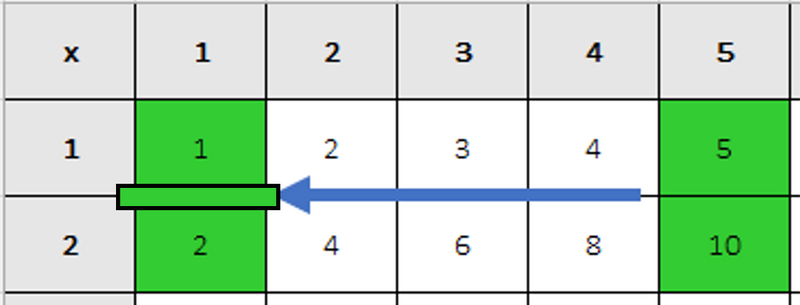
In the example above, the fraction was 5/10. Moving along the rows to the left, you see that 5/10 reduces to 1/2. You know this is correct because 5 is half of 10!
What about larger fractions?
In the example below, the fraction of 28/42 is being reduced. Notice that the numbers aren't directly under each other, but if you move along the rows to the left, you still get the reduced fraction 4/6.
Here's another example:
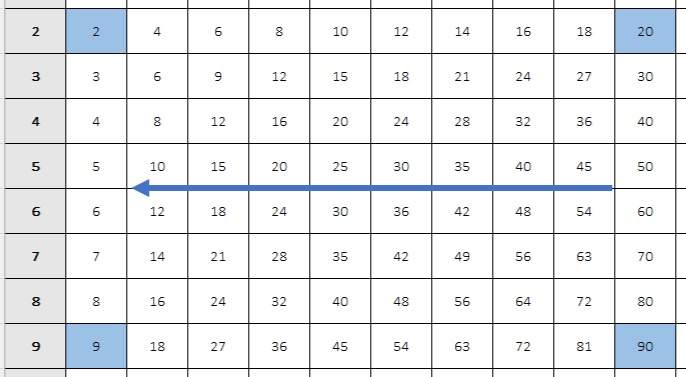
The fraction 20/90 gets reduced to 2/9. See how easy that is!

Challenge
The fraction 4/6 can still be reduced. Can you figure out how by using your multiplication chart?
Quiz
Did you figure out what 4/6 reduces to?
Take Action

Why did the student do multiplication problems on the floor? The teacher told him not to use tables.

You learned how handy a multiplication table can be! Want to learn more about the multiplication table?
Your feedback matters to us.
This Byte helped me better understand the topic.