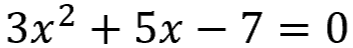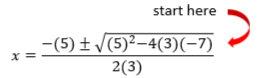You own a company selling apps and you need to know the best selling price for maximum profit. If this quadratic equation could help you find the answer...
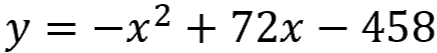
...would you be able to solve it?
Solving quadratic equations is all about finding the "x"!
But First...Some Need to Know Terms!
What is a quadratic equation?
Quadratic comes from the word "quad", which means "square". So, a quadratic function is a polynomial function of a degree of 2. "Polynomial" means the sum of many terms: "poly" (many) and "nomial" (name).
When plotted on a graph, quadratic equations are U-shaped (like a horseshoe) and can open upwards (as in a smiley face) or downwards (as in a sad face).
What are factors?
Factors multiply to get a number.
Factoring is the inverse (or reverse action) of multiplying. For example, when factoring 18, you'll find numbers that multiply to get 18 (1, 2, 3, 6, 9, 18). This is where knowing multiplication tables comes in handy!
What is standard form?
Standard formin math simplifies rules for clear understanding, communication, and computation. Quadratic equations are easier to factor in standard form...
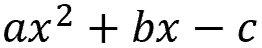
...where "a", "b", and "c" are numbers and "x" is the variable (or unknown).
"a" and "b" are called coefficients — a constant number multiplied by a variable.
"c" is called a constant — it's a fixed value not multiplied by a variable.
If the coefficient is absent, you can understand it to be "1". If "a" = 1, you only need to find the factors of "c". An example of handling a quadratic when "a" > 1 will be provided later.
How are quadratic equations made?
Multiplying binomials is similar to multiplying two-digit numbers. The exception is two algebraic expressions are being multiplied instead of only digits.
The video below provides an example:
Method #1: Factoring
Factoring is the inverse (or reverse operation) of multiplying two algebraic expressions.
Example #1
You have the quadratic equation:
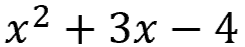
To factor this, you need to identify the algebraic expressions that were multiplied together. Your end result will look like this...
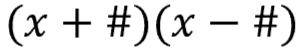
...where "x" is the variable (x that makes x squared) in the equation and "#" will be the factors of 4 (the numbers that multiply to get 4)
The video below explains factoring quadratics a bit further.
One method to finding those factors is using a table:
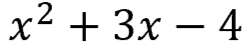
Label a table with the headings Factor, Added, Subtracted. Use the abbreviations "F", "A", and "S".
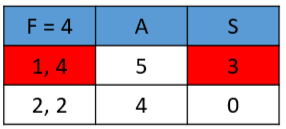Image created by Wendy McMillan, 2016
List factor pairs (of 4) in the Factors (F) column
Add factor pairs in the Added (A) column
Subtract factor pairs in the Subtracted (S) column
Find the answer under heading A or S for the middle term (3).
Answer:
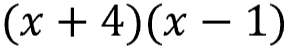
The sign of the middle number determines positive or negative constants. Since the middle number 3 is positive, 4 must be positive (think 4 - 1 vs. 1 - 4).
Example #2
When the value "a" > 1, you'll need to multiply the "a" and "c" values together, then factor.
Take a look at this equation:
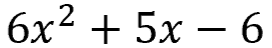
Multiply 6 ("a") x 6 ("c") = 36
Factor 36
You'll see that factors 9 and 4 when subtracted total 5
With "a" and "c" values as 6, further factorize 9 and 4 to form the required factor groups [2 x 2 = 4 and 3 x 3 = 9 so 9 - 4 = 5 and 9 x 4 = 36.]
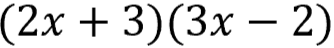
Find "x" by Solving Algebraic Equations
Now that you have your factors, you can find the value of "x".
Set each factor group equal to 0 (zero)
Solve for "x" using the order of operations
Example #1:
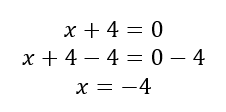
Example #2:
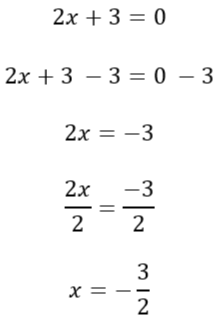
Method #2: Complete the Square
What if you have an algebraic equation like this?
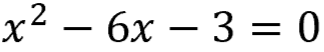
There aren't any factors of 3 that add or subtract to get 6!
You'll need to complete the square — meaning, you'll need to make the formula a perfect square.
You'll do this by:
Rearranging the equation with variables on one side
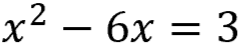
Dividing the "b" term (6) by 2
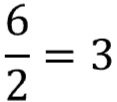
Squaring that answer
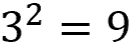
Adding that answer to both sides of the equation
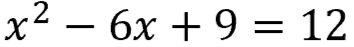
Factor the new equation
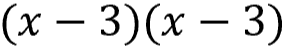
This equation could also be written like this...
...which is why it's called a perfect square!
Method #3: Use the Square Root Property
What about quadratic equations in this form?
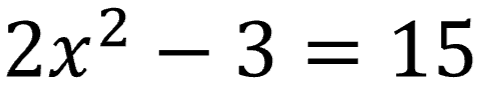
The middle term ("bx") is missing!
You'll need the square root method to solve these types of equations.
Square roots are the inverse or reverse action of squaring a number.
First, isolate "x" by eliminating any coefficients or additive/subtractive terms by adding 3 to both sides, then simplifying
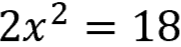
Divide each term by 2
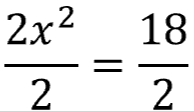
End with this equation
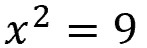
Take the square root of both sides
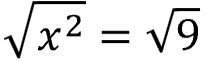
This is where knowing squared numbers comes in handy!
Your result should have a positive AND a negative answer since a negative times negative number and a positive times a positive number both equal a positive answer.
Method #4: Use the Quadratic Formula
Some equations are rebellious and just can't be solved using any of the methods above.
Example:
When the value "a" > 1, multiply the "a" and "c" values, then factor!
3 x 7 = 21....but there are NO factors of 21 (1, 3, 7, 21) that add or subtract to get 5.
Enter the quadratic formula!
GIF created by Wendy McMillian, 2023 with PowerPoint and pngtree.com
In standard equations "a", "b", and "c" will be numerical values. That is:
a = 3
b = 5
c = -7 (don't forget to carry the negative along)
Replace each variable in the quadratic formula with the corresponding number minding all negatives and positives. Use parenthesis to keep things organized!
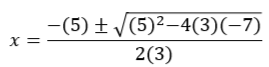
Begin solving under the radical:
End by simplifying:
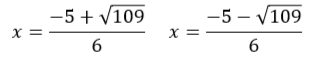
If you enter these equations into a calculator you end up with nasty-looking decimals! It's better to just leave it as a fraction.
Method #5: Graph to Solve the Algebraic Equation and Find "x"
One easy way to solve quadratics is by graphing! Remember the equation at the beginning of this lesson?
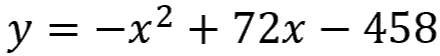No factors of 458 (1, 2, 229, 458) add or subtract to get 72.
These big numbers will cause major headaches too when used in the quadratic formula!
Desmos will save the day!
Desmos is a graphing calculatorthat handles big equations.
Type the equation into Desmos
Zoom out using the "-" button
Find where the graph crosses the x-axis (2 places)
The "x"-values are the factors for the equation
At the beginning of this lesson, you were asked if you could find the best price to sell apps and make a maximum profit.
Graphing videos created by Wendy McMillian using Desmos graphing calculator online and Screencastify
Find the answer by scrolling to the top of the graph to the x-value at the graph's peak — which is 36.
You'll need to sell 36 apps in order to make a profit!
Take Action
Your feedback matters to us.
This Byte helped me better understand the topic.