English
​
Answer:

The mean of the dataset

Did you know?

There are two formulas for variance: one formula is used for calculating population variance, while the other is used for sample variance.

Here is a breakdown of the formulas:

2

Population Variance (σ²): σ² = Σ (xᵢ- µ) ² / N

3

Sample Variance (s²): s² = Σ (xᵢ-µ) ² / (N-1)

4

Sources:

1 https://www.sciencebuddies.org/science-fair-projects/science-fair/variance-and-standard-deviation

2 https://www.cuemath.com/data/variance/

3 https://www.cuemath.com/data/variance/

4 https://www.cuemath.com/data/variance/

Step 1: Find the Mean (μ)

Dataset: [9, 14, 5, 8, 11, 7]

To workout the mean:

  • Add up all the values in the dataset.

  • Divide the sum by the total number of values to find the mean (μ).

A math problem on graph paper. The problem involves working out the mean of 9,14,5,8,and 11 by adding these numbers. Image created by the author using PowerPoint. To hear an audio version of the information in the image above, click the play button on the audio player below:

Quiz

What is the mean of the following dataset: 5, 8, 10, 12, 15.

Answer:

10

Step 2: Calculate the Squared Differences (xᵢ - μ)²

  • For each value (xᵢ), subtract the mean (μ).

  • Square the result of each subtraction to get the squared differences.

A chart: a dataset of values (left column). xᵢ minus μ values (middle column). xᵢ minus μ squared (right column).

Image created by the author using PowerPoint. To hear an audio version of the information in the image above, click the play button on the audio player below:

Quiz

How many steps are there when working out the squared difference?

Answer:

2

Step 3: Sum all the Squared Differences

  • Sum all the squared differences obtained in the previous step.

The same chart from above but with an added column that calculates the total. Image created by the author using PowerPoint. To hear an audio version of the information in the image above, click the play button on the audio player below:

Quiz

The ages (in years) of 4 plants in a greenhouse are: 2, 3, 5, and 7. What is the sum of their squared difference?

Answer:

15

Did you know?

There are limitations of variance. Variance gives extra weight to outliers by squaring deviations, which can mislead in skewed distributions. Additionally, its units are squared, making direct interpretation difficult.

1
Outliers are extreme numerical values, much larger or smaller than other values in the dataset.

Source:

1 https://www.khanacademy.org/math/statistics-probability/summarizing-quantitative-data/variance-standard-deviation-population/v/variance-of-a-population

Step 4: Compute the Variance

  • Divide the sum of squared differences by the total number of values in the dataset to get the variance.

A problem on paper. Σ (xᵢ- µ) ² / N =50 where N=6 and calculation of variance by dividing 50 by 6 giving an answer of 8.33. Image created by the author using PowerPoint. To hear an audio version of the information in the image above, click the play button on the audio player below:

Quiz

Here are the ages of 5 employees. What is their age variance? 30, 45, 20, 50, 35. (Population Variance (σ²): σ² = Σ (xᵢ- µ) ² / N)

Answer:

114

Did you know?

Variance is used in various fields, including finance to determine the volatility of stock returns, in quality control manufacturing to assess consistency, and in climate studies to understand variations in temperature over time.

1

Source:

1 Hayes, Adam. "What Is Variance in Statistics? Definition, Formula, and Example." 19 Dec. 2023, https://www.investopedia.com/terms/v/variance.asp

Take Action

A person working out complex math equations.

Now that you're able to calculate variance, you can take your data analysis a step further by completing the tasks below:

Rumie logo

This logo isn't an ad or affiliate link. It's an organization that shares in our mission, and empowered the authors to share their insights in Byte form.
Rumie vets Bytes for compliance with our Standards. The organization is responsible for the completeness and reliability of the content.
Learn more about how Rumie works with partners.

License:

Ever wonder why weather forecasts give a high and low temperature instead of just one number?

A weatherman holding a green umbrella over his head and pointing at a weather chart. Image courtesy of storyset via Freepik

Imagine you're planning a trip and check the forecast. It says "high of 24 degrees Celsius." Perfect for sightseeing! But then you see another number, "low of 10 degrees Celsius." Brrrr! Maybe pack a jacket after all.

This is where variance comes in! Variance helps us understand how spread out the data points (temperatures in this case) are from the average (the high of 24 degrees Celsius).

Did you know?

24 degrees Celsius is 75.2 degrees Farenheit and 10 degrees Celsius is 50 degrees Farenheit.

Variance Explained

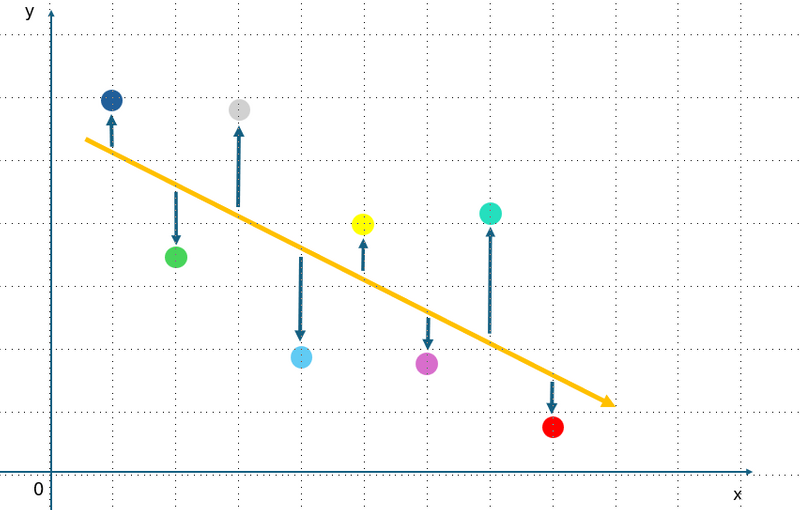An x-y graph showing a straight-line sloping down and arrows pointing from the line towards different colored circles. Image created by author using PowerPoint

Varianceis a measure of how much the values in a dataset differ from the mean (average) of the dataset — the set of numerical values for which you want to determine the spread.

Understanding variance is essential for statistical analysis and helps you understand data distribution.

To calculate the variance, you need to follow this formula:

Variance = Σ(xᵢ - μ)² / N

Where:

  • Σ represents the sum of the numbers in the dataset

  • xᵢ represents each individual value in the dataset

  • μ represents the mean of the dataset

  • N represents the total number of values in the dataset

In other words, the formula can be explained as:

  1. Subtract the mean from each value in the dataset.

  2. Square the result of each subtraction.

  3. Sum all the squared differences.

  4. Divide the sum by the total number of values in the dataset to calculate the variance.

Quiz

What does the symbol μ represent in statistical notation?

Did you know?

There are two formulas for variance: one formula is used for calculating population variance, while the other is used for sample variance.

Here is a breakdown of the formulas:

Population Variance (σ²): σ² = Σ (xᵢ- µ) ² / N

Sample Variance (s²): s² = Σ (xᵢ-µ) ² / (N-1)

Step 1: Find the Mean (μ)

Dataset: [9, 14, 5, 8, 11, 7]

To workout the mean:

  • Add up all the values in the dataset.

  • Divide the sum by the total number of values to find the mean (μ).

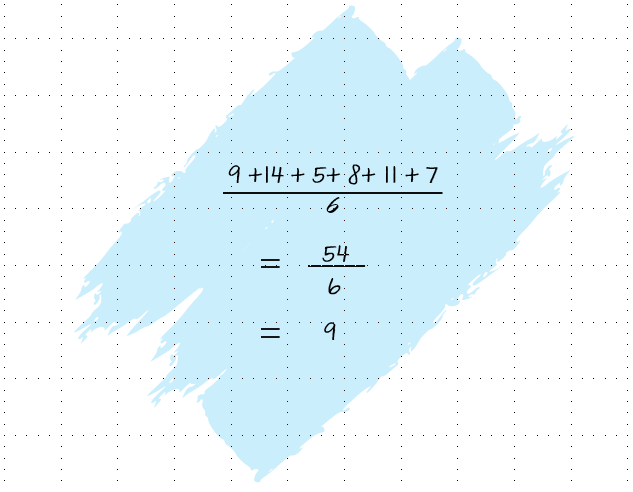A math problem on graph paper. The problem involves working out the mean of 9,14,5,8,and 11 by adding these numbers. Image created by the author using PowerPoint. To hear an audio version of the information in the image above, click the play button on the audio player below:

Quiz

What is the mean of the following dataset: 5, 8, 10, 12, 15.

Subscribe for more quick bites of learning delivered to your inbox.

Unsubscribe anytime. No spam. 🙂

Step 2: Calculate the Squared Differences (xᵢ - μ)²

  • For each value (xᵢ), subtract the mean (μ).

  • Square the result of each subtraction to get the squared differences.

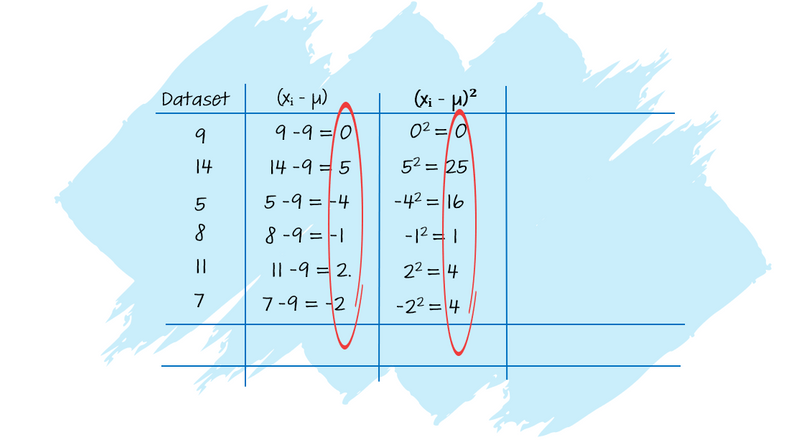
A chart: a dataset of values (left column). xᵢ minus μ values (middle column). xᵢ minus μ squared (right column).

Image created by the author using PowerPoint. To hear an audio version of the information in the image above, click the play button on the audio player below:

Quiz

How many steps are there when working out the squared difference?

Step 3: Sum all the Squared Differences

  • Sum all the squared differences obtained in the previous step.

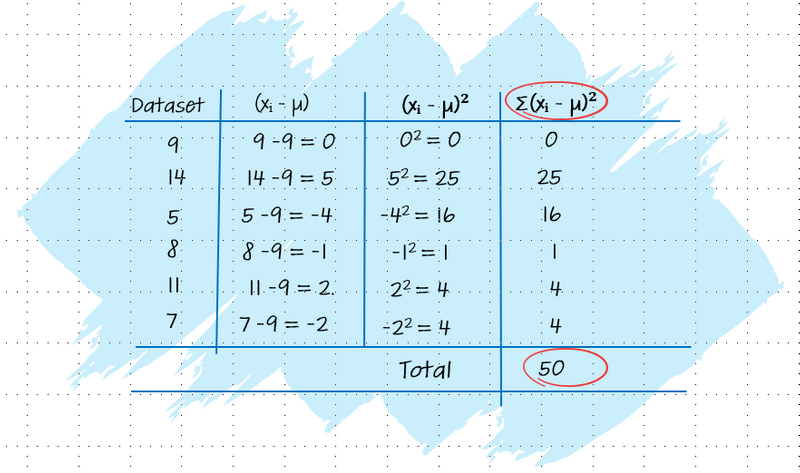The same chart from above but with an added column that calculates the total. Image created by the author using PowerPoint. To hear an audio version of the information in the image above, click the play button on the audio player below:

Quiz

The ages (in years) of 4 plants in a greenhouse are: 2, 3, 5, and 7. What is the sum of their squared difference?

Did you know?

There are limitations of variance. Variance gives extra weight to outliers by squaring deviations, which can mislead in skewed distributions. Additionally, its units are squared, making direct interpretation difficult.

Outliers are extreme numerical values, much larger or smaller than other values in the dataset.

Step 4: Compute the Variance

  • Divide the sum of squared differences by the total number of values in the dataset to get the variance.

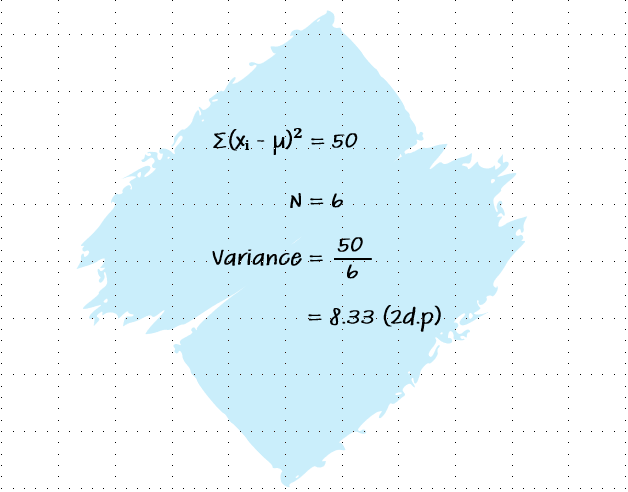A problem on paper. Σ (xᵢ- µ) ² / N =50 where N=6 and calculation of variance by dividing 50 by 6 giving an answer of 8.33. Image created by the author using PowerPoint. To hear an audio version of the information in the image above, click the play button on the audio player below:

Quiz

Here are the ages of 5 employees. What is their age variance? 30, 45, 20, 50, 35. (Population Variance (σ²): σ² = Σ (xᵢ- µ) ² / N)

Did you know?

Variance is used in various fields, including finance to determine the volatility of stock returns, in quality control manufacturing to assess consistency, and in climate studies to understand variations in temperature over time.

Take Action

A person working out complex math equations.

Now that you're able to calculate variance, you can take your data analysis a step further by completing the tasks below:

License:

Your feedback matters to us.

This Byte helped me better understand the topic.

#learning-to-learn

#learning-strategies

#practical-skills

#student

#student-life

#education

#k-12

New Bytes

We publish fresh Bytes daily, we can send you a notification when that happens.

​

Did you know?

There are two formulas for variance: one formula is used for calculating population variance, while the other is used for sample variance.

Here is a breakdown of the formulas:

2

Population Variance (σ²): σ² = Σ (xᵢ- µ) ² / N

3

Sample Variance (s²): s² = Σ (xᵢ-µ) ² / (N-1)

4

Sources:

1 https://www.sciencebuddies.org/science-fair-projects/science-fair/variance-and-standard-deviation

2 https://www.cuemath.com/data/variance/

3 https://www.cuemath.com/data/variance/

4 https://www.cuemath.com/data/variance/

Step 1: Find the Mean (μ)

Dataset: [9, 14, 5, 8, 11, 7]

To workout the mean:

  • Add up all the values in the dataset.

  • Divide the sum by the total number of values to find the mean (μ).

A math problem on graph paper. The problem involves working out the mean of 9,14,5,8,and 11 by adding these numbers. Image created by the author using PowerPoint. To hear an audio version of the information in the image above, click the play button on the audio player below:

Quiz

What is the mean of the following dataset: 5, 8, 10, 12, 15.

Answer:

10

Step 2: Calculate the Squared Differences (xᵢ - μ)²

  • For each value (xᵢ), subtract the mean (μ).

  • Square the result of each subtraction to get the squared differences.

A chart: a dataset of values (left column). xᵢ minus μ values (middle column). xᵢ minus μ squared (right column).

Image created by the author using PowerPoint. To hear an audio version of the information in the image above, click the play button on the audio player below:

Quiz

How many steps are there when working out the squared difference?

Answer:

2

Step 3: Sum all the Squared Differences

  • Sum all the squared differences obtained in the previous step.

The same chart from above but with an added column that calculates the total. Image created by the author using PowerPoint. To hear an audio version of the information in the image above, click the play button on the audio player below:

Quiz

The ages (in years) of 4 plants in a greenhouse are: 2, 3, 5, and 7. What is the sum of their squared difference?

Answer:

15

Did you know?

There are limitations of variance. Variance gives extra weight to outliers by squaring deviations, which can mislead in skewed distributions. Additionally, its units are squared, making direct interpretation difficult.

1
Outliers are extreme numerical values, much larger or smaller than other values in the dataset.

Source:

1 https://www.khanacademy.org/math/statistics-probability/summarizing-quantitative-data/variance-standard-deviation-population/v/variance-of-a-population

Step 4: Compute the Variance

  • Divide the sum of squared differences by the total number of values in the dataset to get the variance.

A problem on paper. Σ (xᵢ- µ) ² / N =50 where N=6 and calculation of variance by dividing 50 by 6 giving an answer of 8.33. Image created by the author using PowerPoint. To hear an audio version of the information in the image above, click the play button on the audio player below:

Quiz

Here are the ages of 5 employees. What is their age variance? 30, 45, 20, 50, 35. (Population Variance (σ²): σ² = Σ (xᵢ- µ) ² / N)

Answer:

114

Did you know?

Variance is used in various fields, including finance to determine the volatility of stock returns, in quality control manufacturing to assess consistency, and in climate studies to understand variations in temperature over time.

1

Source:

1 Hayes, Adam. "What Is Variance in Statistics? Definition, Formula, and Example." 19 Dec. 2023, https://www.investopedia.com/terms/v/variance.asp

Take Action

A person working out complex math equations.

Now that you're able to calculate variance, you can take your data analysis a step further by completing the tasks below:

Rumie logo

This logo isn't an ad or affiliate link. It's an organization that shares in our mission, and empowered the authors to share their insights in Byte form.
Rumie vets Bytes for compliance with our Standards. The organization is responsible for the completeness and reliability of the content.
Learn more about how Rumie works with partners.

License:

Recommended Bytes