Have you ever thought to yourself....
 ...especially fractional exponents!
...especially fractional exponents!
Fractions can be tough to work with when they are just fractions. But when they become exponents, things can get even more complicated — that is, if you don't know the key rules for dealing with fractional exponents!
What are Exponents?

Exponents are actually repeated multiplication —multiplying the same number over and over. Exponents allow you to shortcut repeated multiplication by specifying how many times to multiply a number.
Remember:
The base is the number multiplied.
The exponent tells us how many times to multiply that base.
For example, 2 x 2 x 2 can be rewritten as 2 to the third power or as 2 raised to the third power.
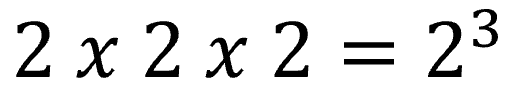
Did you know?
What are Fractional Exponents?
 Fractional exponents are fractions instead of whole numbers, like the example below:
Fractional exponents are fractions instead of whole numbers, like the example below:
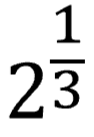 Where a whole number exponent represents repeated multiplication, fractional exponents represent root expressions. The 1/n (n being the denominator, as the 3 in 1/3) represents both a fraction and the exponent.
Where a whole number exponent represents repeated multiplication, fractional exponents represent root expressions. The 1/n (n being the denominator, as the 3 in 1/3) represents both a fraction and the exponent.
The general form of a fractional exponent is b to m/n power, where:
b is the base
m/n is the exponent
m is the numerator
n is the denominator
Transforming Fractional Exponents
 To transform a fractional exponent into a root expression, you need only to know where each part of the fractional exponent goes in a radical sign. Radical signs are the root signs, like this:
To transform a fractional exponent into a root expression, you need only to know where each part of the fractional exponent goes in a radical sign. Radical signs are the root signs, like this:
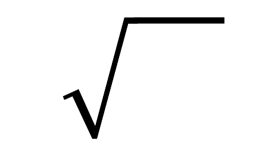 The denominator of the fractional exponent determines the base's root. The numerator raises the base to a power.
The denominator of the fractional exponent determines the base's root. The numerator raises the base to a power.
Like this:
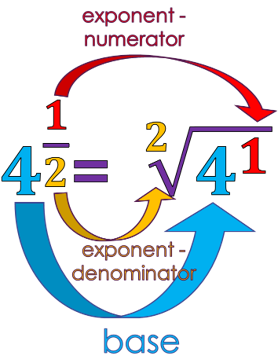
4 to the power of 1/2.
 To hear an audio description of the equation above, press play on the audio player below.
To hear an audio description of the equation above, press play on the audio player below.
The base (4) lands safely inside the radical sign. The numerator (1) raises the base (4) to the power (1). The denominator (2) becomes the root — in this case, the square root.
Here are some more examples:
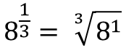 8 raised to the 1/3 power is the cube root of 8, which equals 2.
8 raised to the 1/3 power is the cube root of 8, which equals 2.
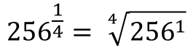 256 raised to the 1/4 power is the fourth root of 256, which equals 4.
256 raised to the 1/4 power is the fourth root of 256, which equals 4.
Here's a table that may help:
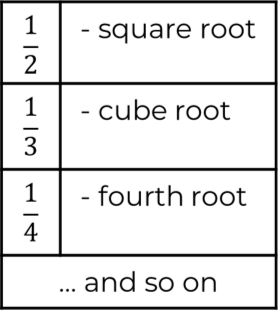 To hear an audio description of the chart above, press play on the audio player below.
To hear an audio description of the chart above, press play on the audio player below.
Subscribe for more quick bites of learning delivered to your inbox.
Unsubscribe anytime. No spam. 🙂
Fractional Exponents with Numerator Greater than 1
 But what happens when the fractional exponent's numerator is greater than one?
But what happens when the fractional exponent's numerator is greater than one?
Glad you asked!
The key rule for dealing with fractional exponents is that:
The numerator raises the base to the power.
The denominator becomes the root (square, cube, etc.).
Raise the base to the power indicated, then take the root of the expression.

Let's see some examples:
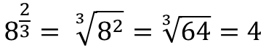
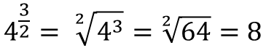
The numerator raises each number to that power (multiply the base that many times).
The denominator takes the root of the number under the radical (find the root of the number).
Quiz
What is the root for 3 raised to the 3/5ths power?
Take Action
 Now that you've learned the key rules for dealing with fractional exponents, you're ready to work those fractional exponent problems!
Now that you've learned the key rules for dealing with fractional exponents, you're ready to work those fractional exponent problems!
But, in case you need more help, take a look at these resources:
Your feedback matters to us.
This Byte helped me better understand the topic.
