This logo isn't an ad or affiliate link. It's an organization that shares in our mission, and empowered the authors to share their insights in Byte form.
Rumie vets Bytes for compliance with our
Standards.
The organization is responsible for the completeness and reliability of the content.
Learn more
about how Rumie works with partners.
Ever wonder why weather forecasts give a high and low temperature instead of just one number?
Image courtesy of storyset via Freepik
Imagine you're planning a trip and check the forecast. It says "high of 24 degrees Celsius." Perfect for sightseeing! But then you see another number, "low of 10 degrees Celsius." Brrrr! Maybe pack a jacket after all.
This is where variance comes in! Variance helps us understand how spread out the data points (temperatures in this case) are from the average (the high of 24 degrees Celsius).
Did you know?
24 degrees Celsius is 75.2 degrees Farenheit and 10 degrees Celsius is 50 degrees Farenheit.
Variance Explained
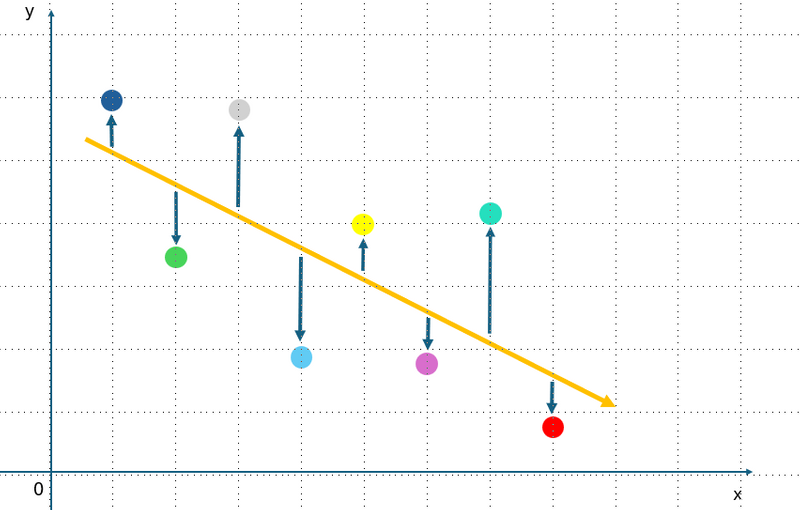Image created by author using PowerPoint
Varianceis a measure of how much the values in a dataset differ from the mean (average) of the dataset — the set of numerical values for which you want to determine the spread.
Understanding variance is essential for statistical analysis and helps you understand data distribution.
Variance = Σ(xᵢ - μ)² / N
Where:
Σ represents the sum of the numbers in the dataset
xᵢ represents each individual value in the dataset
μ represents the mean of the dataset
N represents the total number of values in the dataset
In other words, the formula can be explained as:
Subtract the mean from each value in the dataset.
Square the result of each subtraction.
Sum all the squared differences.
Divide the sum by the total number of values in the dataset to calculate the variance.
Quiz
What does the symbol μ represent in statistical notation?
Subtract the mean from each value in the dataset, then square the result of each subtraction, and finally sum all the squared differences and divide by the total number of values.
Step 1: Find the Mean (μ)
Dataset: [9, 14, 5, 8, 11, 7]
To workout the mean:
Add up all the values in the dataset.
Divide the sum by the total number of values to find the mean (μ).
Image created by the author using PowerPoint. To hear an audio version of the information in the image above, click the play button on the audio player below:
Quiz
What is the mean of the following dataset: 5, 8, 10, 12, 15.
The sum of all values divided by the number of values. Mean = (5 + 8 + 10 + 12 + 15) / 5 = 10
Step 2: Calculate the Squared Differences (xᵢ - μ)²
For each value (xᵢ), subtract the mean (μ).
Square the result of each subtraction to get the squared differences.
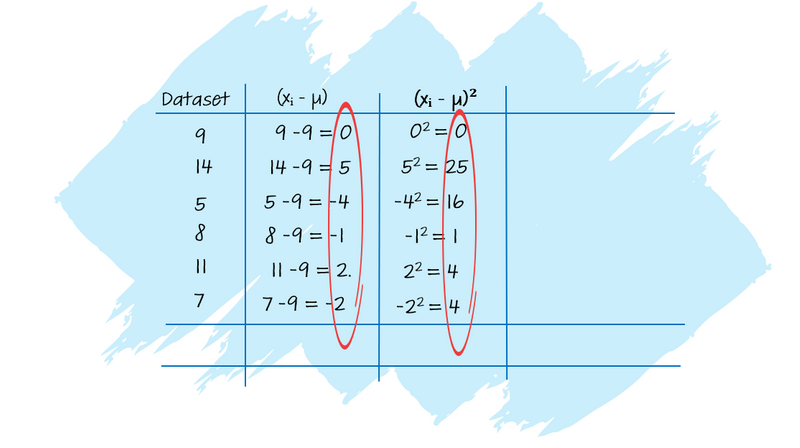
Image created by the author using PowerPoint. To hear an audio version of the information in the image above, click the play button on the audio player below:
Quiz
How many steps are there when working out the squared difference?
For each data point in the dataset, subtract the mean and square the difference. This is done to find the squared deviation for each data point.
Step 3: Sum all the Squared Differences
Sum all the squared differences obtained in the previous step.
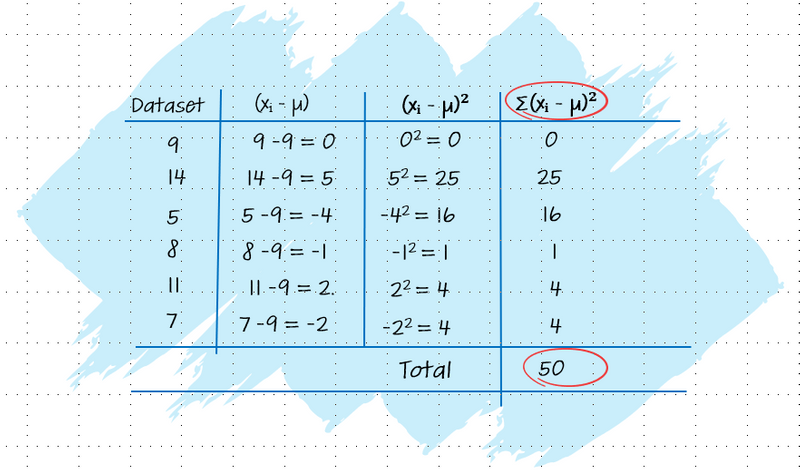Image created by the author using PowerPoint. To hear an audio version of the information in the image above, click the play button on the audio player below:
Quiz
The ages (in years) of 4 plants in a greenhouse are: 2, 3, 5, and 7. What is the sum of their squared difference?
Variance squares the difference of each point from the mean. Extreme values (outliers) have a much larger impact on the final variance compared to data points closer to the mean.
Did you know?
There are limitations of variance. Variance gives extra weight to outliers by squaring deviations, which can mislead in skewed distributions. Additionally, its units are squared, making direct interpretation difficult. Outliers are extreme numerical values, much larger or smaller than other values in the dataset.
Step 4: Compute the Variance
Divide the sum of squared differences by the total number of values in the dataset to get the variance.
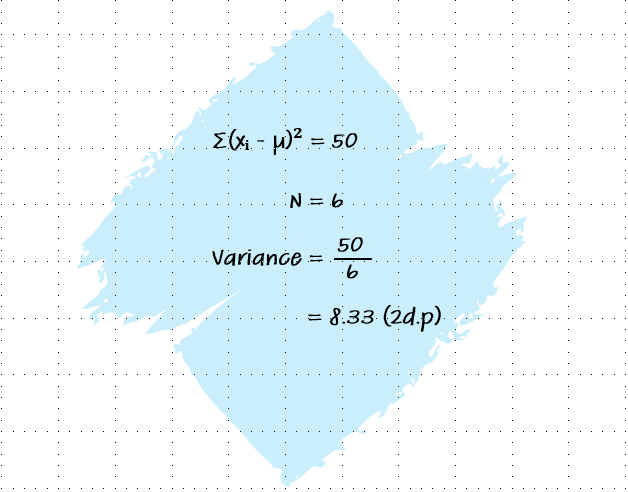Image created by the author using PowerPoint. To hear an audio version of the information in the image above, click the play button on the audio player below:
Quiz
Here are the ages of 5 employees. What is their age variance? 30, 45, 20, 50, 35. (Population Variance (σ²): σ² = Σ (xᵢ- µ) ² / N)
1. Calculate the mean of the dataset. 2. For each data point, subtract the mean and square the result. 3. Sum all the squared differences. 4. Divide the sum of squared differences by the total number of data points. 5. The result is the population variance.
Did you know?
Variance is used in various fields, including finance to determine the volatility of stock returns, in quality control manufacturing to assess consistency, and in climate studies to understand variations in temperature over time.
Take Action
Now that you're able to calculate variance, you can take your data analysis a step further by completing the tasks below:
This Byte has been authored by
reggie alex moon
Teacher
MA,BSc(Hons)