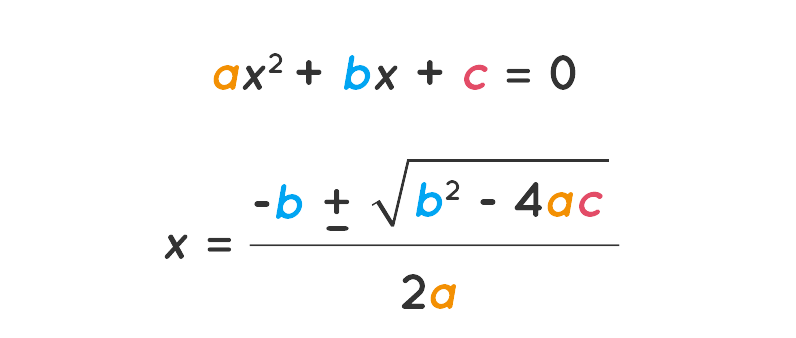This logo isn't an ad or affiliate link. It's an organization that shares in our mission, and empowered the authors to share their insights in Byte form.
Rumie vets Bytes for compliance with our
Standards.
The organization is responsible for the completeness and reliability of the content.
Learn more
about how Rumie works with partners.
Quadratic equations can seem intimidating, but they don’t have to be!
Learning to solve equations by factoring is a powerful tool that can make math much easier and even a bit fun.
Learn to break it down step-by-step, so you can confidently tackle any quadratic equation that comes your way!
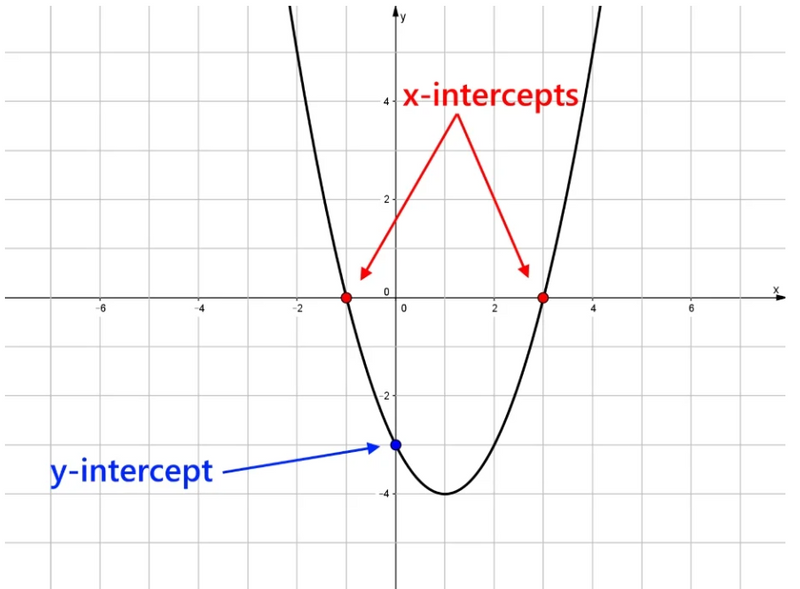
Essentials of Quadratic Equations
Standard Form:
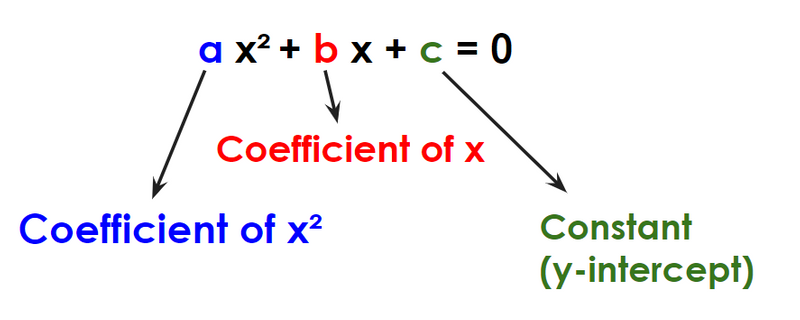
Factored Form:
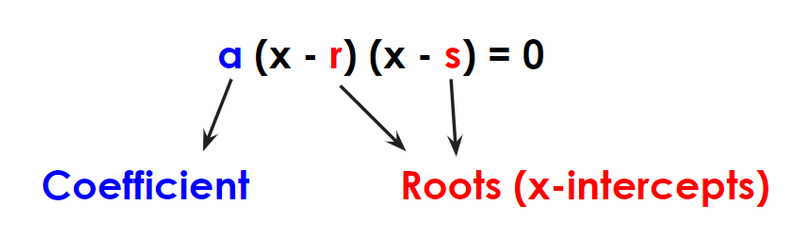
Images created by the author using Google Slides
Solving Quadratics:
To solve quadratic equations, the goal is to get the equation into factored form and find what x is equal to. To get to factored form from standard form, you'll use a method called factoring.
Preparing to Factor
There are a few things to consider before you solve equations by factoring:
Always be to factor out the Greatest Common Factor, if there is one.
If a = 1, you can use the Sum-Product Method.
If a ≠ 1, you can use Decomposition.
There are special cases of Perfect Square Trinomials and Difference of Squares that have their own rules.
The Quadratic Formula will always give you the value of x if you're unable to factor.
Image created by the author using WordArt
Did you know?
Rumie is a nonprofit community dedicated to making innovative learning free for everyone.
1. Common Factoring
ALWAYS start any factoring method by finding the Greatest Common Factor (GCF) of the terms in the quadratic and pulling it out.
Step 1: Find the Greatest Common Factor. Check out How to Find the Greatest Common Factor if you need a refresher.
Step 2: Divide the terms by the GCF.
Step 3: Pull the GCF out of the expression and leave the divided terms in the brackets.
Example:
10x³ + 30x² + 55x
Images in this Byte were created by the author using Google Slides. To hear audio descriptions of these images, click play on the audio player below each image:
Quiz
Factor the GCF out from 8x² - 12x + 16:
The GCF of 8x², 12x, and 16 is 4. Divide each term by 4 and pull it out of the expression: 4(2x² - 3x + 4). Ensure all signs stay the same.
2. Sum-Product Method when a = 1
The Sum-Product Method is all about finding two numbers (r and s) that add up b (the coefficient of x) and multiply to c (the constant term). This method can only be used when a = 1 in ax² + bx + c.
Step 1: Find all the pairs of numbers that multiply to c. This includes negative numbers.
Step 2: Determine which pair adds up to get b.
Step 3: Plug the pair (r and s) into (x + r)(x + s) = 0.
Step 4: Find the x values that make the expression true (i.e., where x + r = 0 and x + s = 0).
Example:
x² - 7x + 12
a = 1
b = -7
c = 12
Quiz
Solve x² + 2x - 8 using the Sum-Product method:
-2 and 4 are the values that multiply to get -8 and add to get 2. The factored expression is (x - 2)(x + 4). Set the expression equal to 0 and solve for x: (x - 2) = 0 and (x + 4) = 0, giving x = 2 and x = -4.
3. Decomposition Method when a ≠ 1
The process of decomposition is breaking up the middle term in the expression and using grouping to fully factor. Use this method when you have more complex quadratics, such as when a ≠ 1.
If you need a reminder on how to group expressions, check out Factor a Quadratic Equation by Grouping Terms.
Step 1: Find all the pairs of numbers that multiply to (a)(c).
Step 2: Determine which factor pair (r and s) adds to get b.
Step 3: Break the middle term of the expression (bx) into rx and sx.
Step 4: Group each half of the expression and factor out the GCFS.
Step 5: Factor the GCF bracket out of the expression.
Step 6: Set the expression equal to 0 and solve for x.
Example:
Let's look at 2x² + 7x + 5
a = 2
b = 7
c = 5
Quiz
Solve 7x² + 3x - 10 using decomposition.
-7 and 10 are the values that multiply to (7)(-10) = -70 and add to get 3. Break up the middle term: 7x² - 7x + 10x - 10. Factoring by grouping: 7x(x - 1) + 1(x - 1) = (x - 1)(7x + 1). Set the expression equal to 0 and solve for x: (x - 1) = 0 and (7x + 1) = 0 gives x = 1 and x = -0.14.
4. Special Cases
Sometimes, quadratic equations fall into special categories that allow for quick and easy factoring. Recognizing these cases can save you time and effort!
Perfect Square Trinomials
Perfect Square Trinomials have two square terms (a² and b²) with the third term 2ab.
They follow the pattern:
a² + 2ab + b² = (a + b)²
a² - 2ab + b² = (a - b)²
Examples:
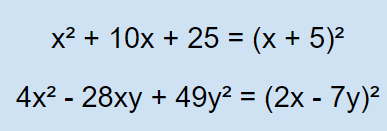
Difference of Squares
Difference of Squares have two square terms (a² and b²) separated by a minus sign.
They follow the pattern:
a² - b² = (a + b) (a - b)
Examples:
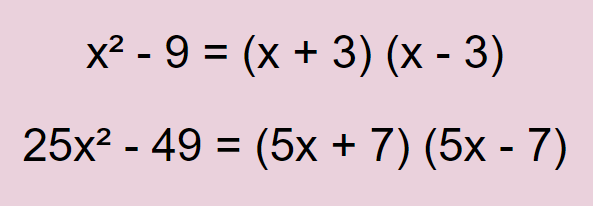
Quiz
Solve 4x² - 36.
Factor out the GCF: 4(x² - 9). Factor using difference of squares: 4(x - 3)(x + 3). Set the equation to 0 and solve for x: (x + 3) = 0 and (x - 3) = 0, giving us that x = -3 and x = 3.
5. Quadratic Formula
When solving equations by factoring gets tricky or when you can't find nice numbers to work with, the quadratic formula comes to the rescue! It allows you to find the solutions for any quadratic equation, no matter how complicated.
Step 1: Sub the values of a, b, and c into the quadratic formula.
Step 2: Solve for x.
Example:
5x² + 10x + 4
a = 5
b = 10
c = 4
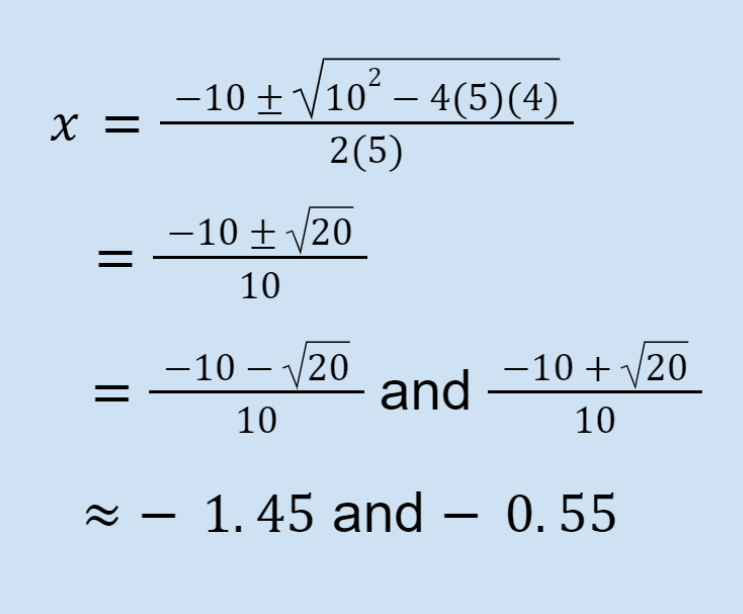The solution is x = -1.45, -0.55.
Quiz
Solve 6x² + 25x + 14 using the quadratic formula:
Substitute the values a = 6, b = 25, and c = 14 into the quadratic formula: [-25 ± √(25² - 4(6)(14))] / 2(6) = (-25 ± √289) / 12 = -3.5, -0.67.
Take Action
It can be tricky to learn a new concept but the most important thing is to take it step by step and PRACTICE. Practice makes perfect!
Not that you know how to solve quadratic equations by factoring:
This Byte has been authored by
Christina DaCosta
AI Trainer
Bsc, BEd